GÖK CİSİMLERİ İLE ENLEM TAYİNİ:
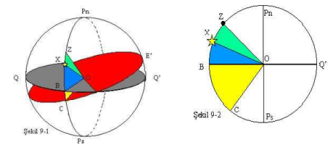
Gök cisimleri meridyenimizde bulunduğunda yani LHA=0° olduğunda daha önce öğrendiğimiz bazı kavramları şekil 9-1 üzerinde tekrar tanımlayalım. PN ve PS gök kutupları,QQ’ gri düzlem gök ekvatorudur. Bu şekilden bir kesit alalım ve şekil 9-2 de gösterelim.

a) XOB açısı mavi taralı açı gök cisminin gök ekvatorundan açısal yükselimidir ki biz buna yükselim (Declination) kısaca dec. diyoruz ve bu değer almanaklarda mevcuttur.
b) Z noktasını başucu olarak biliyoruz.
c) EE’ kırmızı düzlem gözlemcinin ufuk düzlemidir.
d) XOC açısı sarı ve mavi açıların toplamı gök cisminin ufuk düzleminden olan açısal yükselimidir ki biz bu açıyı sekstant ile ölçerek elde ederiz. Açısal yükselim o gün içinde meridyen geçişinde en yüksek değeri alır.
e) ZOB açısı mavi ve yeşil açıların toplamı ise gözlemcinin enlemidir.
Bu şekillerdeki özel duruma A durumu diyelim ve özelliği açıklayalım. Gözlemci ve gök cismi aynı yarı kürede ve gözlemcinin enlemi gök cisminin yükseliminden büyüktür.
Şimdi ZOX açısını veya ZX yayını hesaplayalım. ZX mesafesi daha önceden bildiğimiz başucu mesafesidir. Gök cisminin ufuk düzleminden olan açısal yükselimi yani sekstant ile ölçtüğümüz yükselimden hataları düzelterek bulduğumuz değer gerçek açısal yükselim (Ho) idi.
O halde şekil-1’den; ZX= 90 -Ho yazılır.
Son adım olarak
A durumunda; Lat=Dec.+ZX yazarız.
Bu hesaplamalar için en başta söylediğimiz durum gök cisminin meridyenimizde oluşu idi. Burada dikkat edilmesi gereken; enlemin bulunması için boylamın doğru bir şekilde tespit edilmesidir. Boylamdaki hatalar enlemin hatalı tespitine yol açar. Bu özel durum ile ilgili veriler almanakta bulunmaktadır.
Enlem veya meylin birbirine göre büyüklüğü şöyle tesbit edilir;
Kuzey yarı küredeki gözlemci güneye dönerek(180° ye),
Güney yarı küredeki gözlemci kuzeye dönerek(000° ye),ölçüm yaparsa Lat>dec olur.
ÖRNEK:9 Mayıs 1996 günü güneşin alt kenarından meridyen geçişinde yapılan gözlemde Sex.Alt=58°42’.8 bulunmuştur. Boylamımız Long=032°45’E ve yaklaşık enlemimiz Lat 48°30’N alet hatası IE=+2.1 ve gözlemcinin göz yüksekliği 15 metredir. Enlemi bulunuz.
1.Adım : Boylamın zamana çevrilmesi:
32°--------2h08m
45’-------- 3m
32°45’----2h11m
2.Adım : 9 Mayıs sayfasından meridyen geçişi LMT alınır. UT’ye çevrilir.
LMT -----11h56m
Long------ 2h11m
UT--------09h45m
3.Adım : UT ile 9 Mayıs sayfasında güneşin dec. hesaplanır.
9 Mayıs 09h için dec. N17°28’.4
d=0.6 ve 45m için düz.+ 0.5
9 Mayıs 09h45m dec. N17°28’.9
4.Adım : Ho.bulunur.
Sex.Alt.---58°42’.8
IE ---------+ 2’.1
Obs.Alt----58°44’.9
Dip -------- - 6’.8
App.Alt.---58°38’.1
Main Corr.-+ 15’.4
Ho--------- 58°53’.5
5.Adım : ZX hesaplanır.
ZX=90°- Ho=90°-58°53’.5 ZX=31°06’.5
6.Adım : Enlem hesaplanır. Enlem ve dec aynı isimde N ve Lat>dec.A durumu:
Lat=Dec. + ZX=17°28’.9 + 31°06’.5 Lat=48°35’.4N bulunur.
Özel durum B
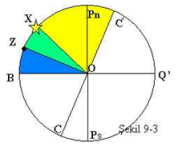
Bu durumda enlem ve yükselim aynı isimde olmakla beraber yükselim enlemden büyüktür. Şekil 9-3
Enlem veya meylin birbirine göre büyüklüğü şöyle tesbit edilir;
Durum B Lat ve dec.aynı isimde Dec.>Lat
ZX=90 – Ho Lat=Dec. – ZX
Kuzey yarı küredeki gözlemci kuzeye dönerek(000° ye),
Güney yarı küredeki gözlemci güneye dönerek(180° ye),ölçüm yaparsa dec>lat olur.
ÖRNEK:11 Mayıs 1996 günü venüs gezegeninin üst meridyen geçişinde yapılan gözlemde Sex.Alt=85°42’.7 bulunmuştur. Yaklaşık konum Lat 23°30’N ve Long 063°45’W alet hatası IE +2’.8 ve göz yüksekliği 10 metredir. Enlemi bulun ?
Gerçek açısal yükselim hesaplanır;
Sex.Alt 85°42’.7
IE + 2’.8
Obs.Alt 85°45’.5
Dip - 5’.6
App.Alt 85°39’.9
Main corr - -0’.1
85°39’.8
Paralax + 0’.0
Ho 85°39’.8
Boylam zamana çevrilir ve Meridyen geçişi UT hesaplanır;
63° 4h12m LMT 14h30m
45’ - 3m Long +4h15m
63°45’ 4h15m UT 18h45m
UT ile 11 Mayıs sayfasından dec. hesaplanır ;
11 Mayıs 18h için dec. N27°38’.7
d=0’.1 ve 45m için düz + 0’.1
11 Mayıs 18h45m dec. N27°38’.8
Başucu mesafesi ve Enlem hesaplanır;
ZX=90° - Ho = 90 - 85°39’.8 = 4°20’.2
Lat=Dec – ZX = 27°38’.8 - 4°20’.2 =23°18’.6N
Lat=23°18’.6N

Gök cisimleri meridyenimizde bulunduğunda yani LHA=0° olduğunda daha önce öğrendiğimiz bazı kavramları şekil 9-1 üzerinde tekrar tanımlayalım. PN ve PS gök kutupları,QQ’ gri düzlem gök ekvatorudur. Bu şekilden bir kesit alalım ve şekil 9-2 de gösterelim.
a) XOB açısı mavi taralı açı gök cisminin gök ekvatorundan açısal yükselimidir ki biz buna yükselim (Declination) kısaca dec. diyoruz ve bu değer almanaklarda mevcuttur.
b) Z noktasını başucu olarak biliyoruz.
c) EE’ kırmızı düzlem gözlemcinin ufuk düzlemidir.
d) XOC açısı sarı ve mavi açıların toplamı gök cisminin ufuk düzleminden olan açısal yükselimidir ki biz bu açıyı sekstant ile ölçerek elde ederiz. Açısal yükselim o gün içinde meridyen geçişinde en yüksek değeri alır.
e) ZOB açısı mavi ve yeşil açıların toplamı ise gözlemcinin enlemidir.
Bu şekillerdeki özel duruma A durumu diyelim ve özelliği açıklayalım. Gözlemci ve gök cismi aynı yarı kürede ve gözlemcinin enlemi gök cisminin yükseliminden büyüktür.
Şimdi ZOX açısını veya ZX yayını hesaplayalım. ZX mesafesi daha önceden bildiğimiz başucu mesafesidir. Gök cisminin ufuk düzleminden olan açısal yükselimi yani sekstant ile ölçtüğümüz yükselimden hataları düzelterek bulduğumuz değer gerçek açısal yükselim (Ho) idi.
O halde şekil-1’den; ZX= 90 -Ho yazılır.
Son adım olarak
A durumunda; Lat=Dec.+ZX yazarız.
Bu hesaplamalar için en başta söylediğimiz durum gök cisminin meridyenimizde oluşu idi. Burada dikkat edilmesi gereken; enlemin bulunması için boylamın doğru bir şekilde tespit edilmesidir. Boylamdaki hatalar enlemin hatalı tespitine yol açar. Bu özel durum ile ilgili veriler almanakta bulunmaktadır.
A durumu Lat ve Dec.aynı isimde
ve Lat.>Dec Lat=Dec.+ZX
ve Lat.>Dec Lat=Dec.+ZX
Enlem veya meylin birbirine göre büyüklüğü şöyle tesbit edilir;
Kuzey yarı küredeki gözlemci güneye dönerek(180° ye),
Güney yarı küredeki gözlemci kuzeye dönerek(000° ye),ölçüm yaparsa Lat>dec olur.
ÖRNEK:9 Mayıs 1996 günü güneşin alt kenarından meridyen geçişinde yapılan gözlemde Sex.Alt=58°42’.8 bulunmuştur. Boylamımız Long=032°45’E ve yaklaşık enlemimiz Lat 48°30’N alet hatası IE=+2.1 ve gözlemcinin göz yüksekliği 15 metredir. Enlemi bulunuz.
1.Adım : Boylamın zamana çevrilmesi:
32°--------2h08m
45’-------- 3m
32°45’----2h11m
2.Adım : 9 Mayıs sayfasından meridyen geçişi LMT alınır. UT’ye çevrilir.
LMT -----11h56m
Long------ 2h11m
UT--------09h45m
3.Adım : UT ile 9 Mayıs sayfasında güneşin dec. hesaplanır.
9 Mayıs 09h için dec. N17°28’.4
d=0.6 ve 45m için düz.+ 0.5
9 Mayıs 09h45m dec. N17°28’.9
4.Adım : Ho.bulunur.
Sex.Alt.---58°42’.8
IE ---------+ 2’.1
Obs.Alt----58°44’.9
Dip -------- - 6’.8
App.Alt.---58°38’.1
Main Corr.-+ 15’.4
Ho--------- 58°53’.5
5.Adım : ZX hesaplanır.
ZX=90°- Ho=90°-58°53’.5 ZX=31°06’.5
6.Adım : Enlem hesaplanır. Enlem ve dec aynı isimde N ve Lat>dec.A durumu:
Lat=Dec. + ZX=17°28’.9 + 31°06’.5 Lat=48°35’.4N bulunur.
Özel durum B
Bu durumda enlem ve yükselim aynı isimde olmakla beraber yükselim enlemden büyüktür. Şekil 9-3
Enlem veya meylin birbirine göre büyüklüğü şöyle tesbit edilir;
Durum B Lat ve dec.aynı isimde Dec.>Lat
ZX=90 – Ho Lat=Dec. – ZX
Kuzey yarı küredeki gözlemci kuzeye dönerek(000° ye),
Güney yarı küredeki gözlemci güneye dönerek(180° ye),ölçüm yaparsa dec>lat olur.
ÖRNEK:11 Mayıs 1996 günü venüs gezegeninin üst meridyen geçişinde yapılan gözlemde Sex.Alt=85°42’.7 bulunmuştur. Yaklaşık konum Lat 23°30’N ve Long 063°45’W alet hatası IE +2’.8 ve göz yüksekliği 10 metredir. Enlemi bulun ?
Gerçek açısal yükselim hesaplanır;
Sex.Alt 85°42’.7
IE + 2’.8
Obs.Alt 85°45’.5
Dip - 5’.6
App.Alt 85°39’.9
Main corr - -0’.1
85°39’.8
Paralax + 0’.0
Ho 85°39’.8
Boylam zamana çevrilir ve Meridyen geçişi UT hesaplanır;
63° 4h12m LMT 14h30m
45’ - 3m Long +4h15m
63°45’ 4h15m UT 18h45m
UT ile 11 Mayıs sayfasından dec. hesaplanır ;
11 Mayıs 18h için dec. N27°38’.7
d=0’.1 ve 45m için düz + 0’.1
11 Mayıs 18h45m dec. N27°38’.8
Başucu mesafesi ve Enlem hesaplanır;
ZX=90° - Ho = 90 - 85°39’.8 = 4°20’.2
Lat=Dec – ZX = 27°38’.8 - 4°20’.2 =23°18’.6N
Lat=23°18’.6N